Le but de cette contribution est d’analyser la conception philosophique de la notion d’inconnue telle qu’elle était utilisée pour la résolution des équations mathématiques durant la période classique négro-africaine.

Nous n’allons pas ici insister sur la définition de la nature exclusive des mathématiques. Nous renvoyons bien à propos à l’excellent article du docte Pr. Kossivi Adjamagbo de l’Université de Paris VI (dit quartier latin…), Docteur d’Etat en Mathématiques, consacré à l’origine africaine des Mathématiques. En effet d’après le témoignage d’Aristote de Stagire dans Métaphysique Livre I, les Egypto-nubiens, autochtones de la Vallée du Nil en sont les inventeurs exclusifs avant sa diffusion au reste du monde. Ces derniers les concevaient conformément

à cette formule consacrée que tout le monde sait maintenant : « Méthode correcte d’investigation dans la nature pour connaître tout ce qui existe, chaque mystère, tous les secrets » et qui figure dans le titre du papyrus hiératique de Rhind selon la traduction du Pr. Obenga in Philosophie africaine de la période pharaonique…p. 357. Ce papyrus daté de -1650 environ est ainsi appelé, comme c’est souvent le cas, et pour cause, à cause du nom de l’Ecossais Alexander Henry Rhind qui l’avait acheté au 19ème siècle à Louxor. Il s’agit d’une copie d’un document plus ancien qui, selon son propre rédacteur le scribe Iamessou, remonte au règne de Nemaatrê Amenamhat III, pharaon-prêtre sem vêtu de peau de léopard, soit vers -1800.

Nous nous donnons d’appuyer le but de notre propos à travers deux exemples de résolution d’équations.

La notion d’abstraction étant difficile, les pédagogues (c’est-à-dire ceux qui guident l’enfant sur la voie de la connaissance et par extension tout néophyte) se servent d’une matérialisation lors des procédés d’apprentissage. C’est ainsi que par exemple, pour apprendre à compter et à faire des opérations simples de calcul, il n’est pas rare que des bâtonnets ou des boules ou tout autres objets soient utilisés comme support afin de matérialiser ce qui se pourrait concevoir plus tard en esprit seulement.

Les mathématiques actuelles utilisent habituellement les lettres latines x, y ou z… souvent pour représenter des inconnues. On remarquera qu’en soit, cela n’est pas endoxal au sens de la logique aristotélicienne. Comme si les modernes se trouvaient incapables de rechercher l’inconnue sans la se représenter de quelque manière. Ceci constituerait une hérésie mathématique pour le kamite de l’époque pharaonique, puisqu’une fois représenté, ce n’est plus une inconnue au sens strict de l’acception. En effet, pour les mathématiciens kamites, une inconnue est une inconnue et rien d’autre. Ce n’est ni x, ni y, ni z…, ni aucune lettre d’aucun système scriptural, ni rien, ni même le néant encore moins une quelconque symbolisation comme on dirait de Dieu, oui c’est bien de cela qu’il s’agit en somme. Le mathématicien kamite peut seulement conjecturer, si nous le pouvons ainsi dire, qu’il est à la quête d’un « mystère », d’un « secret » de quelque chose de caché qu’il se veut révéler. Qu’il s’agisse d’une grandeur numérique commensurable ou non, de tout autre chose ayant ou non une quantifiabilité et ce, que cette inconnue existe ou non, ce qu’en langage moderne, nous disons équation ayant ou non une solution possible, proposition indécidable…

Le génie kamite pose à cet effet ce remarquable postulat: la fameuse inconnue est un multiple de l’Unité. C’est en cela que se trouve l’épaisseur et la consistance de son niveau d’abstraction et non dans aucune autre représentation théorisée de quelque façon. Se faisant, se trouve ainsi baissé, le niveau d’abstraction des modernes. Par exemple selon le mathématicien kamite, pour les grandeurs numériques, que ce soit dans l’ensemble des entiers naturels N, des entiers relatifs Z, des rationnels Q, des réels R ou des complexes C, la valeur sera un multiple de l’Unité ou le quotient de cette même Unité. Ceci nous permet d’entrevoir la puissance de l’Unité et du nombre tout court. En effet, l’un se dit wa en langue pharaonique ; cela lève partiellement le voile sur le caractère divin du concept : il existe des patronymes théophores comme Waenrê qui veut dire l’Unique de Rê comme Akhenaton par exemple. Des textes disent du Créateur Je suis l’Unique devenu le Multiple ou aux Multiples Bras évoquant par-là les millions de millions d’hypostases et autres manifestations cosmiques du Créateur. C’est bien ceci qui a fait dire au néophyte Pythagore de Samos, initié durant 22 ans à Kemet à la Connaissance, que « Tout est Nombre ». C’est un autre sujet qui ne relève pas du but de ce propos.

Venons-en aux exemples d’équations :

Exemple n° 1 tiré du papyrus Rhind: il s’agit du problème numéro R26.

« Quel est le nombre dont la quatrième partie, lorsqu’on la lui ajoute devient 15 ? »

Dans les mathématiques modernes, cela revient à résoudre l’équation du premier degré posée comme suit dans lequel le nombre recherché est représenté par x:

x + (1/4)x = 15 d’où (5/4)x = 15 donc x =(15*4)/5=60/5= 12

Le nombre recherché est donc 12 et on a 12 +12/4= 15 CQFD

Méthode d’opérer kamite :

Compte avec 4

Calcule le quart, à savoir 1

Total 5

Divise 15 par 5

Le résultat est 3

Multiplie 3 par 4

Le résultat est 12

C’est 12 qui s’exprime ainsi. Son quart est 3 qui ajouté à 12 font bien 15 C’EST BIEN CELA (origine du « CE QU’IL FALLAIT DÉMONTRER »).

On observera à l’examen attentif ici que l’inconnue n’est conçue que dans l’esprit du mathématicien qui la se postule de compter avec 4 sans la se représenter d’aucune manière. Nous sommes dans une abstraction pure d’esprit, portée à son plus haut niveau de symbolisation, c’est-à-dire immatériel, subtile, ineffable, approximant ainsi le monde divin où tout est esprit. Certains égyptologues par légèreté et mal inspirés se sont mal à propos égarés de considérer cette méthode comme empirique, naïve, misérable l’allant jusqu’à qualifier par arrogance et inconséquence d’anti-scientifique ! On peut craindre qu’ils n’aient, par le « miracle grec » de Renan, été abusés et noter leur ignorance des dépositions des Anciens Grecs eux-mêmes.

Exemple n°2 tiré du papyrus 6619 de Berlin portant sur une équation du deuxième degré :

« Comment diviser 100 en deux parties pour que la racine carrée de l’une d’entre elles soit les trois quarts de celle de l’autre ? »

Comme pour l’exemple n°1, nous solutionnons le problème à la manière des modernes :

x et y étant les deux inconnues, on posera en langage mathématique actuel par exemple que :

x + y = 100

√x= (3/4) √y   autrement dit, x = (9/16)y

On a donc (9/16)y + y = 100  et (25/16)y = 100, d’où y = 64

On en déduit que x = 36.  On a bien √36  = 6 et √64 = 8 et 6 = ¾ de 8.

Autre méthode moderne de procéder :

X + Y = 100   avec   X = x2   et   Y = y2

On peut alors poser conformément à l’énoncé ce qui suit:

x2 + y2 = 100

4x – 3y = 0  (x=3/4 y c’est-à-dire √X=3/4√Y)

La résolution de ce qui précède donne les mêmes résultats.

Méthode d’opérer kamite :

Comme à l’accoutumée le mathématicien kamite postule que ces mystérieuses inconnues sont des multiples de l’unité.

Alors, il suppose le cas où l’une est l’unité, l’autre sera simplement les 3/4 de cette même unité autrement dit ½ + ¼.

La somme des carrés des deux inconnues sera alors :

1² + (1/2+1/4)²

Soit                              1 + (1/4+1/4+1/16) = 1 +1/2+1/16

Il se trouve que c’est une « identité remarquable » de (1 + 1/4)²   c’est-à-dire (a+ b)²   =   a²  + 2ab + b²

Or c’est justement cette somme des deux carrés qui doit faire 100 autrement dit 10²

On en vient à identifier que : l’inconnue unitaire multipliée par (1 + 1/4) doit être égale à 10 d’où la solution est égale à 8 et 3/4 de 8 est égal à 6. « C’est bien cela » dira le scribe royal de la Maison de Vie.

Tout étant nombre, voici en langage figuré ce que tout ce jargon mathématique veut dire :

    

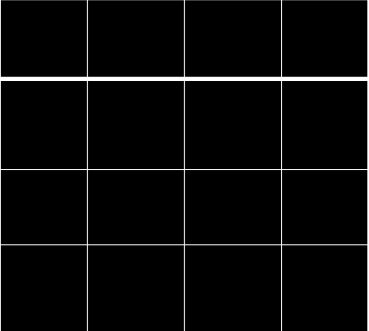
En noir à gauche l’inconnue assimilée à 1 et à droite en rouge celle dont la racine carrée est des 3/4 de celle de la première.

Cela revient à poser le problème en des termes suivants : nous recherchons deux aires de deux carrés tels que d’une part le côté (la racine carrée) de l’un soit les 3/4  de celui de l’autre, les deux aires additionnées devant par ailleurs être égales à 100. Le mathématicien kamite qui possède une abstraction portée à son plus haut niveau part d’un carré de côté une coudée, un pied, un pouce, un mètre, un mile, un « tout système de mesure de distance que l’on voudra » et conduit un raisonnement algébrique magistral. En additionnant les deux aires, on obtient 1 + 9/16 comme l’indiquent les figures ci-dessus. En extrayant la racine carrée de la somme des deux aires on obtient (1 + 1/4). Se pose dès lors une question simplifiée : Quel est le nombre dont l’ajout de son quart donne 10? La réponse est 8. Puissiez-vous reconnaître le problème 26 du fameux papyrus du scribe Iamessou (Rhind). Amon est Grand.

On saisit ici comment le kamite est le premier de tous les hommes à avoir perçu la puissance du nombre. Et ce n’est pas les propos désobligeants du Président raciste Jefferson d’Amérique sur l’esprit nègre qui serait imperméable selon lui aux mathématiques qui résisteront au tempérament nègre que nous venons d’exposer. Et on peut multiplier les exemples à travers la centaine d’énoncés des papyrus Rhind, de Moscou, de Kahoun…

En poussant un peu plus, nous voyons sous nos yeux ici énoncé de manière plus immatérielle et subtile à travers le problème que nous venons d’examiner sur le papyrus de Berlin 6619, ce qui sera plus tard attribué au néophyte Pythagore de Samos comme étant son théorème. Puisque 8² + 6² = 10^2. 

Mieux encore, en comptant manuellement les petits carreaux noirs de gauche et ceux rouges de droite, on obtient :

16 + 9 = 25

C’est-à-dire 4² + 3² = 5² c’est bien cela la Magie du Nombre car on retrouve ainsi sous nos yeux exposé, le triplet kamite (3 -4 -5). C’est ainsi qu’il faudra le nommer dorénavant et pas autrement.

Les subterfuges de privation des Africains de leur héritage ont fait marteler le théorème de Pythagore comme issu du génie indo-européen. Sauf que deux observations s’imposent de façon indestructible : 1- Pythagore de Samos (d’ailleurs d’Asie Mineure en Ionie), de son vrai nom Némakos, n’a jamais publié un seul traité de mathématiques ni de philosophie, lui qui se présentait comme tel à ses concitoyens grecs à son retour d’Egypte ; et sa vie n’est connue que grâce aux doxographes (les on dit) dont son élève Jamblique ; 2- le papyrus ici évoqué date de l’époque de Séthy premier, fondateur de la 19^ème dynastie, celle de Ramsès II, soit plus de 8 siècles avant notre adepte de la Pythie héliopolitaine. Sauf à nous apporter la preuve que Pythagore a émis son théorème avant d’avoir vécu, les faits resteront têtus. Du reste le mot de l’énigme nous viendra de Clément d’Alexandrie qui affirme dans son Stroma qu’un livre de 1000 pages ne suffirait pas à recenser les emprunts que ses compatriotes grecs ont faits aux Kamites.

Or dans « La géométrie égyptienne », Théophile Obenga avait démontré en s’appuyant sur le problème numéro R49 du papyrus de Rhind que le théorème dit de Pythagore existait plus de 1000 ans avant ce dernier à travers ce que les Kamites appelaient le triangle sacré (droit) de côtés 3-4-5. Si nous remontons autour des -1800 du document original, plus de 1300 ans séparent alors les attestations initiales antérieures à l’auteur proclamé du fameux théorème. Mieux encore, depuis l’Ancien Empire l’usage de la corde à 13 nœuds issue de ce théorème était en vogue dans la construction des pyramides. Dans ces conditions, et ce comme pour l’invention de l’Ecriture, ceux qui veulent évoquer, sur la base de la fameuse tablette argileuse Plimpton 322, d’interprétation douteuse et datée de plus de 1000 ans avant Pythagore, l’origine mésopotamienne de ce théorème, doivent revoir leurs arguments. Et nous pouvons fournir des éléments plus anciens encore. En plus des autres triplets sacrés dits pythagoriciens attestés dans les papyrus mathématiques. Selon Diop lui-même, tous les éléments de civilisation qui génèrent tant de ferveur pharaomaniaque actuellement étaient déjà présents depuis l’époque de Djoser et Imhotep de Memphis.

C’est ici l’occasion de produire ce passage du Traité d’Isis et d’Osiris de Plutarque au chapitre 56 et profiter pour inviter à méditer le Grand Hymne à Amon notamment à partir du chapitre 100, le Trop Mystérieux de Qui il n’existe aucun témoignage parfait sur l’aspect :

« Il paraît probable que c’est au plus beau des triangles, au triangle rectangle, que les Égyptiens assimilent spécialement la nature de l’Univers; et, du reste, c’est de ce triangle que Platon semble s’être servi dans sa République (Poltique), pour représenter le mariage sous une forme rectiligne. Dans ce triangle rectangle, un des côtés de l’angle droit est représenté par 3 ; la base l’est par 4, et l’hypoténuse, par 5. Or le carré de celle-ci est égal à la somme des carrés faits sur les deux côtés qui contiennent l’angle droit. Il faut donc concevoir, que le côté de l’angle droit représente le mâle, que la base du triangle représente la femelle, et que l’hypoténuse est le produit des deux; qu’ainsi Osiris est le premier principe, qu’Isis en reçoit les influences, et que Horus est le résultat de l’opération de l’un et de l’autre. En effet 3 est le premier nombre impair et parfait ; 4 est le carré de 2, premier nombre pair; et 5, qui est composé de 3 et de 2, tient à la fois et de son père et de sa mère. Du mot pente (cinq) est dérivé le mot « panta » « univers », ainsi que le verbe « pempazô », qui signifie « compter avec les cinq doigts ». De plus, 5 élevé au carré donne un nombre égal à celui des lettres de leur alphabet et à celui des années que vivait le bœuf Apis. Les Égyptiens ont donc coutume d’appeler Horus Caimin, ce qui répond à « vu », parce que ce monde est sensible et visible. Pour Isis, elle est appelée tantôt Muth, tantôt Athyri, tantôt Methyer. Le premier de ces noms signifie mère, le deuxième, habitation d’Horus en ce monde (dans le même sens que Platon a dit « l’espace est le récipient de la génération ») ; le troisième est composé de deux mots qui veulent dire plein et cause : car la matière du monde est pleine, et elle se rattache à une cause essentiellement pure et bien ordonnée.

Alors, nous pouvons conclure humblement qu’il n’est point de connaissance des mystères et secrets de la Nature certes cachés comme Amon Lui-Même sans la Mathématique, la Vraie telle qu’elle fut inventée.